Which noise model is the best to capture the distinct GWAS phenotypes?

Author

Saikat Banerjee

Published

August 9, 2023

Abstract
We label the GWAS phenotypes to visualize the separation of the principal components of the low rank approximation of the input matrix. For low rank approximation, we use the three methods we have developed till date.

Getting Setup

Code 
import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
from pymir import mpl_stylesheet
from pymir import mpl_utils
mpl_stylesheet.banskt_presentation(splinecolor = 'black', dpi = 120, colors = 'kelly')

from nnwmf.optimize import IALM
from nnwmf.optimize import FrankWolfe, FrankWolfe_CV
from nnwmf.utils import model_errors as merr

import sys
sys.path.append("../utils/")
import histogram as mpy_histogram
import simulate as mpy_simulate
import plot_functions as mpy_plotfn

Loading data

Code 
data_dir = "../data"
beta_df_filename   = f"{data_dir}/beta_df.pkl"
prec_df_filename   = f"{data_dir}/prec_df.pkl"
se_df_filename     = f"{data_dir}/se_df.pkl"
zscore_df_filename = f"{data_dir}/zscore_df.pkl"

'''
Data Frames for beta, precision, standard error and zscore.
'''

beta_df   = pd.read_pickle(beta_df_filename)
prec_df   = pd.read_pickle(prec_df_filename)
se_df     = pd.read_pickle(se_df_filename)
zscore_df = pd.read_pickle(zscore_df_filename)

trait_df = pd.read_csv(f"{data_dir}/trait_meta.csv")
phenotype_dict = trait_df.set_index('ID')['Broad'].to_dict()
Code 
zscore_df
AD_sumstats_Jansenetal_2019sept.txt.gz CNCR_Insomnia_all GPC-NEO-NEUROTICISM IGAP_Alzheimer Jones_et_al_2016_Chronotype Jones_et_al_2016_SleepDuration MDD_MHQ_BIP_METACARPA_INFO6_A5_NTOT_no23andMe_... MDD_MHQ_METACARPA_INFO6_A5_NTOT_no23andMe_noUK... MHQ_Depression_WG_MAF1_INFO4_HRC_Only_Filtered... MHQ_Recurrent_Depression_WG_MAF1_INFO4_HRC_Onl... ... ieu-b-7 ieu-b-8 ieu-b-9 ocd_aug2017.txt.gz pgc-bip2021-BDI.vcf.txt.gz pgc-bip2021-BDII.vcf.txt.gz pgc-bip2021-all.vcf.txt.gz pgc.scz2 pgcAN2.2019-07.vcf.txt.gz pts_all_freeze2_overall.txt.gz
rs1000031 -0.999531 -0.327477 1.241557 0.441709 -0.163658 0.163658 -0.336654 -0.793129 -1.075357 -2.182304 ... 0.532189 NaN NaN -0.198735 1.057089 -0.269020 1.279776 -0.433158 -1.573766 -1.674269
rs1000269 -1.212805 -1.046310 0.741814 -1.844296 -2.673787 -1.126391 0.092067 0.163246 1.643581 2.122280 ... 1.665179 -0.732000 -0.699000 0.100883 -0.226381 0.338368 -0.924392 0.832016 0.681645 -0.701776
rs10003281 -0.813444 2.034345 -1.750164 -0.076778 -0.954165 1.805477 NaN NaN NaN NaN ... -0.475795 4.437998 2.366001 0.967399 0.286699 -1.162661 -0.199299 0.014539 NaN -1.379710
rs10004866 0.011252 1.327108 1.442363 -1.215173 -0.050154 -1.439531 2.458370 2.407460 -0.001038 -1.678331 ... -1.234375 -2.520001 -0.593997 -0.685110 0.902252 1.106939 1.776456 -1.654677 -0.964630 0.851608
rs10005235 0.612540 -0.410609 0.653087 0.344062 -2.183486 1.514102 -0.460191 -0.393006 1.015614 0.180744 ... 0.387805 -0.345000 -0.960998 0.177317 -1.339598 1.795867 -1.249969 2.349671 0.996305 -0.333356
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
rs9989571 0.028306 -0.208891 0.366470 0.821257 0.453762 -1.895698 0.218149 0.920789 1.581000 1.121551 ... -1.231511 -0.820996 0.712000 -2.150176 -0.877410 -1.938969 -2.729983 3.207917 1.469194 -1.293122
rs9991694 -0.679790 -1.005571 0.753472 -0.539271 1.674665 -2.862736 -3.744820 -3.583060 -4.072853 -2.804192 ... 0.064417 NaN NaN -2.884911 -1.000231 0.031860 -1.248222 2.309425 NaN 1.048454
rs9992763 0.691405 -0.010299 -0.140010 -0.419843 -0.138304 0.568052 0.019684 -0.194404 0.869694 0.061210 ... 0.191860 -0.074000 1.030997 -0.228287 -0.051297 0.781766 0.010638 0.456681 -0.503370 -1.435277
rs9993607 -1.625392 -0.391585 0.514268 0.027576 0.150969 -0.113039 -4.638940 -4.631950 -2.918354 -2.204015 ... -0.685106 0.194000 0.240001 -0.790290 -0.876804 -0.577696 -0.785670 -0.062707 0.240834 -0.199740
rs999494 -0.303642 0.872613 -0.227674 1.390424 0.138304 1.281552 1.873050 1.645590 1.381878 -0.010875 ... -0.437500 0.253000 -0.926997 -1.449674 0.910515 0.783853 1.376043 -5.195746 -1.151316 0.660120

10068 rows × 69 columns

X_nan = np.array(zscore_df).T
X_nan_cent = X_nan - np.nanmean(X_nan, axis = 0, keepdims = True)
X_nan_mask = np.isnan(X_nan)
X_cent = np.nan_to_num(X_nan_cent, copy = True, nan = 0.0)

print (f"We have {X_cent.shape[0]} samples (phenotypes) and {X_cent.shape[1]} features (variants)")
print (f"Fraction of Nan entries: {np.sum(X_nan_mask) / np.prod(X_cent.shape):.3f}")
We have 69 samples (phenotypes) and 10068 features (variants)
Fraction of Nan entries: 0.193
select_ids = zscore_df.columns
labels = [phenotype_dict[x] for x in select_ids]
unique_labels = list(set(labels))
nsample = X_cent.shape[0]
ntrait  = len(unique_labels)

trait_indices = [np.array([i for i, x in enumerate(labels) if x == label]) for label in unique_labels]
trait_colors  = {trait: color for trait, color in zip(unique_labels, (mpl_stylesheet.kelly_colors())[:ntrait])}

We perform PCA (using SVD) on the raw input data (mean centered). In Figure 1, we look at the proportion of variance explained by each principal component.

Code 
U, S, Vt = np.linalg.svd(X_cent, full_matrices = False)
S2 = np.square(S)
pcomp = U @ np.diag(S)

fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.plot(np.arange(S.shape[0]), np.cumsum(S2 / np.sum(S2)), 'o-')
plt.show()
Figure 1: Proportion of variance explained by the principal components of the input matrix

In Figure 2, we look at the proportion of variance for each trait explained by the first principal component. Traits in the same “broad category” are combined together to show the histogram (boxplot).

Code 
fig = plt.figure(figsize = (12, 6))
ax1 = fig.add_subplot(111)


pcidx = 0
tot_variance  = S2[pcidx]
trait_scores  = [np.square(pcomp[idx, pcidx]) / tot_variance for idx in trait_indices]

def rand_jitter(n, d = 0.1):
    return np.random.randn(n) * d

for ilbl, label in enumerate(unique_labels):
    xtrait = trait_scores[ilbl]
    nsample = xtrait.shape[0]
    
    boxcolor = trait_colors[label]
    boxface = f'#{boxcolor[1:]}80' #https://stackoverflow.com/questions/15852122/hex-transparency-in-colors
    medianprops = dict(linewidth=0, color = boxcolor)
    whiskerprops = dict(linewidth=2, color = boxcolor)
    boxprops = dict(linewidth=2, color = boxcolor, facecolor = boxface)
    flierprops = dict(marker='o', markerfacecolor=boxface, markersize=3, markeredgecolor = boxcolor)
    
    ax1.boxplot(xtrait, positions = [ilbl],
                showcaps = False, showfliers = False,
                widths = 0.7, patch_artist = True, notch = False,
                flierprops = flierprops, boxprops = boxprops,
                medianprops = medianprops, whiskerprops = whiskerprops)
    
    ax1.scatter(ilbl + rand_jitter(nsample), xtrait, edgecolor = boxcolor, facecolor = boxface, linewidths = 1)


ax1.axhline(y = 0, ls = 'dotted', color = 'grey')
ax1.set_xticks(np.arange(len(unique_labels)))
ax1.set_xticklabels(unique_labels, rotation = 90)
ax1.set_ylabel(f"PC{pcidx + 1:d}")

plt.show()
Figure 2: Trait-wise PVE by the first principal component of the input matrix
Code 
def plot_stacked_bars(ax, data, xlabels, colors, bar_width = 1.0, alpha = 1.0):
    '''
    Parameters
    ----------
        data: 
            dict() of scores. 
            - <key> : items for the stacked bars (e.g. traits)
            - <value> : list of scores for the items. All dict entries must have the same length of <value>
        xlabels: 
            label for each entry in the data <value> list. Must be of same length of data <value>
        colors: 
            dict(<key>, <color>) corresponding to each data <key>.
    '''
    indices = np.arange(len(xlabels))
    bottom = np.zeros(len(xlabels))

    for item, weights in data.items():
        ax.bar(indices, weights, bar_width, label = item, bottom = bottom, color = colors[item], alpha = alpha)
        bottom += weights

    ax.set_xticks(indices)
    ax.set_xticklabels(xlabels)

    for side, border in ax.spines.items():
        border.set_visible(False)

    ax.tick_params(bottom = True, top = False, left = False, right = False,
                   labelbottom = True, labeltop = False, labelleft = False, labelright = False)
    
    return

def get_trait_pc_scores(U, S, tindices, ulabels, min_idx = 0, max_idx = 20, use_proportion = False):
    '''
    Prepare data for stacked bars
    Parameters
    ----------
        U: left singular vectors
        S: singular values
        tindices: [np.array(<index of samples in class>)], length = number-of-classes
        ulabels: name of classes, length = number-of-classes
    '''
    scores = dict()
    pcindices = np.arange(min_idx, max_idx)
    pcomp = U @ np.diag(S)
    S2 = np.square(S)
    
    for pcidx in pcindices:
        scores[pcidx] = [np.square(pcomp[idx, pcidx]) for idx in tindices]
        if use_proportion:
            scores[pcidx] = [x / S2[pcidx] for x in scores[pcidx]]# divide by total variance
            
    # Create data for input to stacked bars
    data = {trait: [np.sum(scores[idx][ilbl]) for idx in pcindices] for ilbl, trait in enumerate(ulabels)}
            
    return data

def quick_plot_trait_pc_scores(X, tindices, ulabels, tcolors, min_idx = 0, max_idx = 20):
    '''
    Quick helper function to plot the same thing many times
    '''
    X_cent = mpy_simulate.do_standardize(X, scale = False)
    U, S, Vt = np.linalg.svd(X_cent, full_matrices = False)
    
    data = get_trait_pc_scores(U, S, tindices, ulabels, min_idx = min_idx, max_idx = max_idx, use_proportion = False)
    data_scaled = get_trait_pc_scores(U, S, tindices, ulabels, min_idx = min_idx, max_idx = max_idx, use_proportion = True)
    xlabels = [f"{i + 1}" for i in np.arange(min_idx, max_idx)]

    fig = plt.figure(figsize = (12, 10))
    ax1 = fig.add_subplot(211)
    ax2 = fig.add_subplot(212)
    plot_stacked_bars(ax1, data, xlabels, tcolors, alpha = 0.8)
    plot_stacked_bars(ax2, data_scaled, xlabels, tcolors, alpha = 0.8)

    ax1.legend(bbox_to_anchor=(1.04, 1), loc="upper left")

    ax2.set_xlabel("Principal Components")
    ax1.set_ylabel("Trait-wise scores for each PC")
    ax2.set_ylabel("Trait-wise scores for each PC (scaled)")
    plt.tight_layout(h_pad = 2.0)
    plt.show()
    return

In Figure 3, we stack the variance score of each disease category for each principal component. Components explaining majority of the same disease are able to distinguish the corresponding disease.

Code 
quick_plot_trait_pc_scores(X_cent, trait_indices, unique_labels, trait_colors)
Figure 3: Trait-wise PVE for the first 20 principal components of the input matrix

Denoising methods

IALM - RPCA

Code 
rpca = IALM(max_iter = 1000, mu_update_method='admm', show_progress = True)
rpca.fit(X_cent, mask = X_nan_mask)
2023-08-08 23:52:50,980 | nnwmf.optimize.inexact_alm               | DEBUG   | Fit RPCA using IALM (mu update admm, lamba = 0.0100)
2023-08-08 23:52:51,174 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 0. Primal residual 0.893741. Dual residual 0.000574896
2023-08-08 23:52:58,800 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 100. Primal residual 6.36112e-05. Dual residual 2.55942e-05
2023-08-08 23:53:06,396 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 200. Primal residual 2.26287e-05. Dual residual 2.64972e-06
2023-08-08 23:53:13,952 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 300. Primal residual 6.03351e-06. Dual residual 1.69738e-06
2023-08-08 23:53:21,531 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 400. Primal residual 4.08978e-06. Dual residual 8.33885e-07
2023-08-08 23:53:29,124 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 500. Primal residual 3.12383e-06. Dual residual 5.16786e-07
2023-08-08 23:53:36,784 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 600. Primal residual 2.50002e-06. Dual residual 3.39206e-07
2023-08-08 23:53:44,356 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 700. Primal residual 2.03607e-06. Dual residual 3.14692e-07
2023-08-08 23:53:51,946 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 800. Primal residual 8.29061e-07. Dual residual 5.20502e-07
2023-08-08 23:53:59,570 | nnwmf.optimize.inexact_alm               | INFO    | Iteration 900. Primal residual 4.70128e-07. Dual residual 2.64999e-07
Code 
np.linalg.matrix_rank(rpca.L_)
50
Code 
np.linalg.norm(rpca.L_, 'nuc')
1351.8480150432197
Code 
np.sum(np.abs(rpca.E_)) / np.prod(X_cent.shape)
0.590626180741227

FW - NNM

Also check how the cross-validation works

Code 
nnmcv = FrankWolfe_CV(chain_init = True, reverse_path = False, debug = True, kfolds = 5)
nnmcv.fit(X_nan_cent)
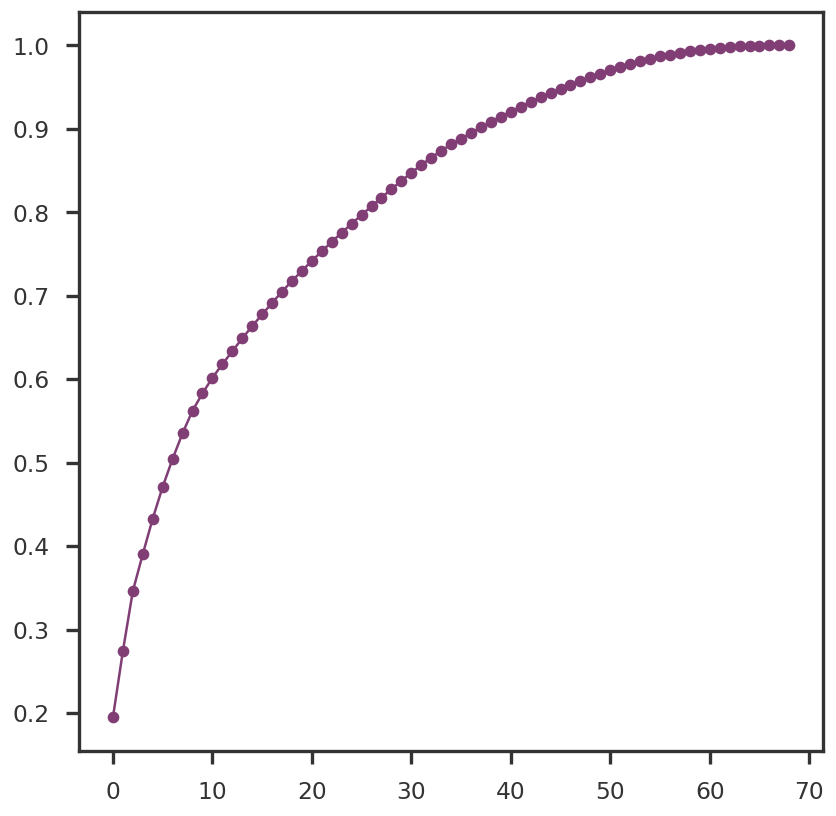
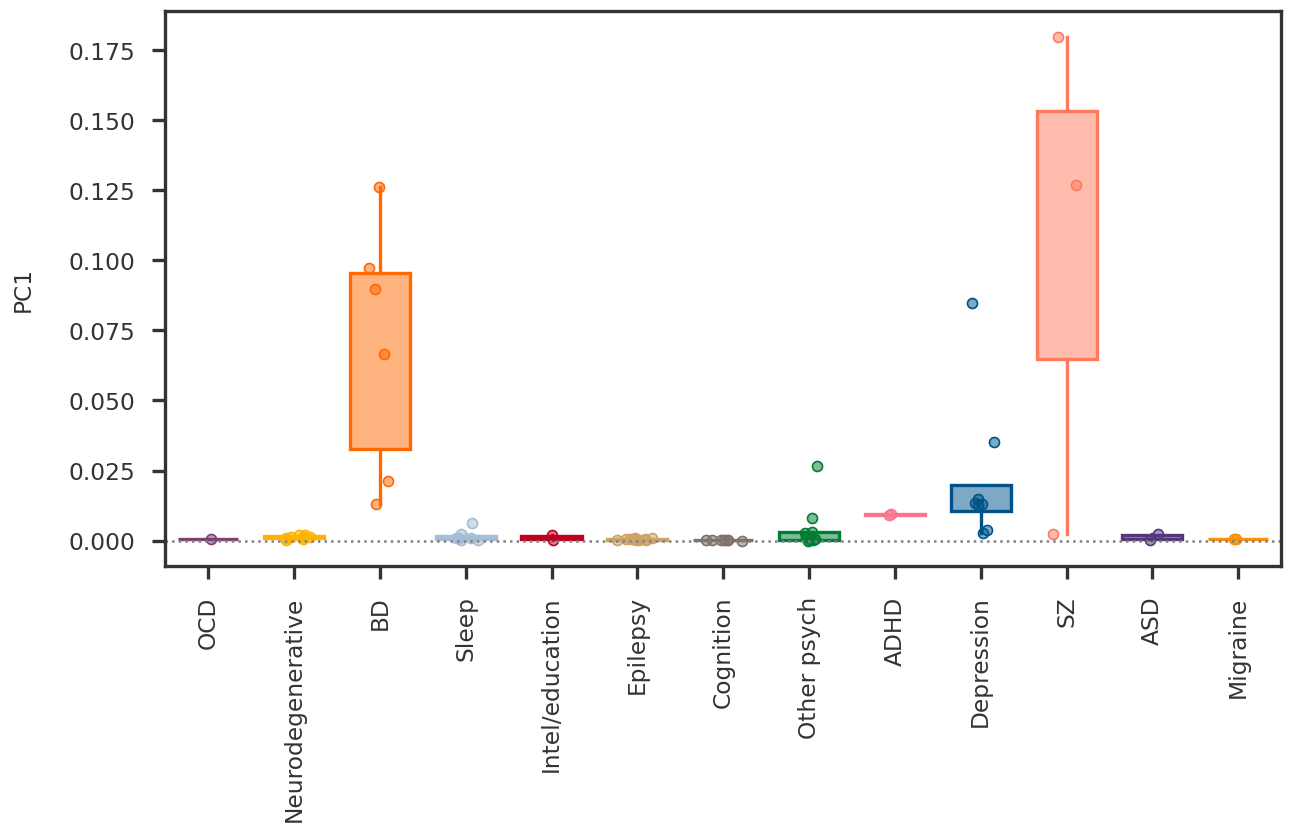
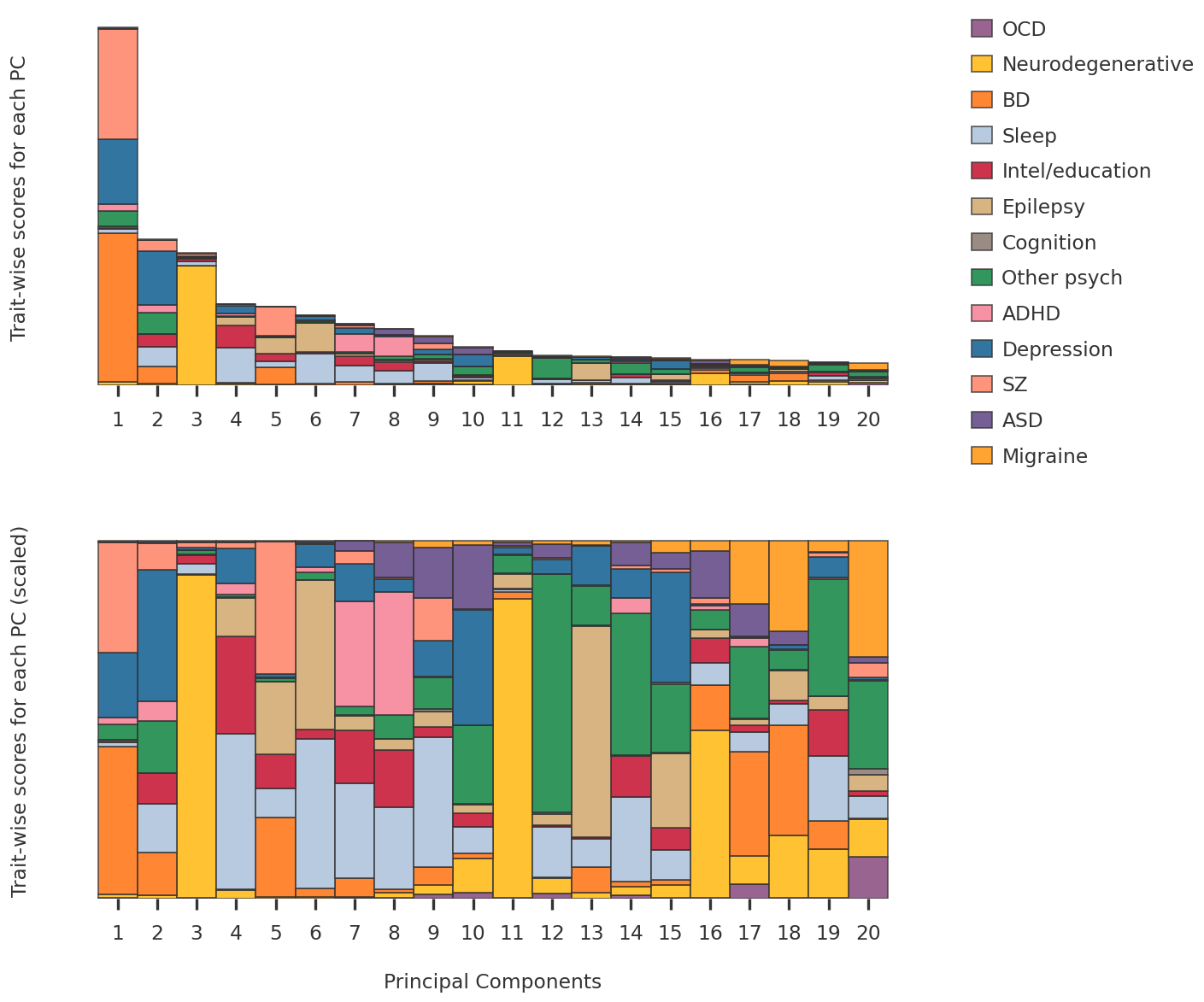
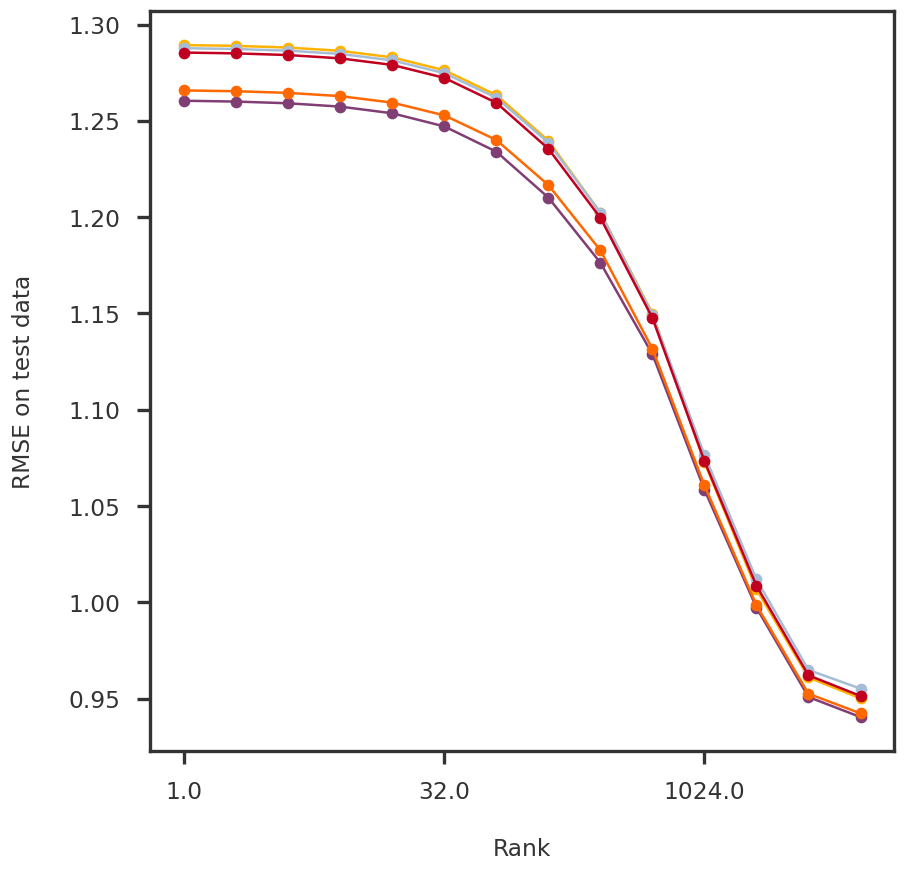
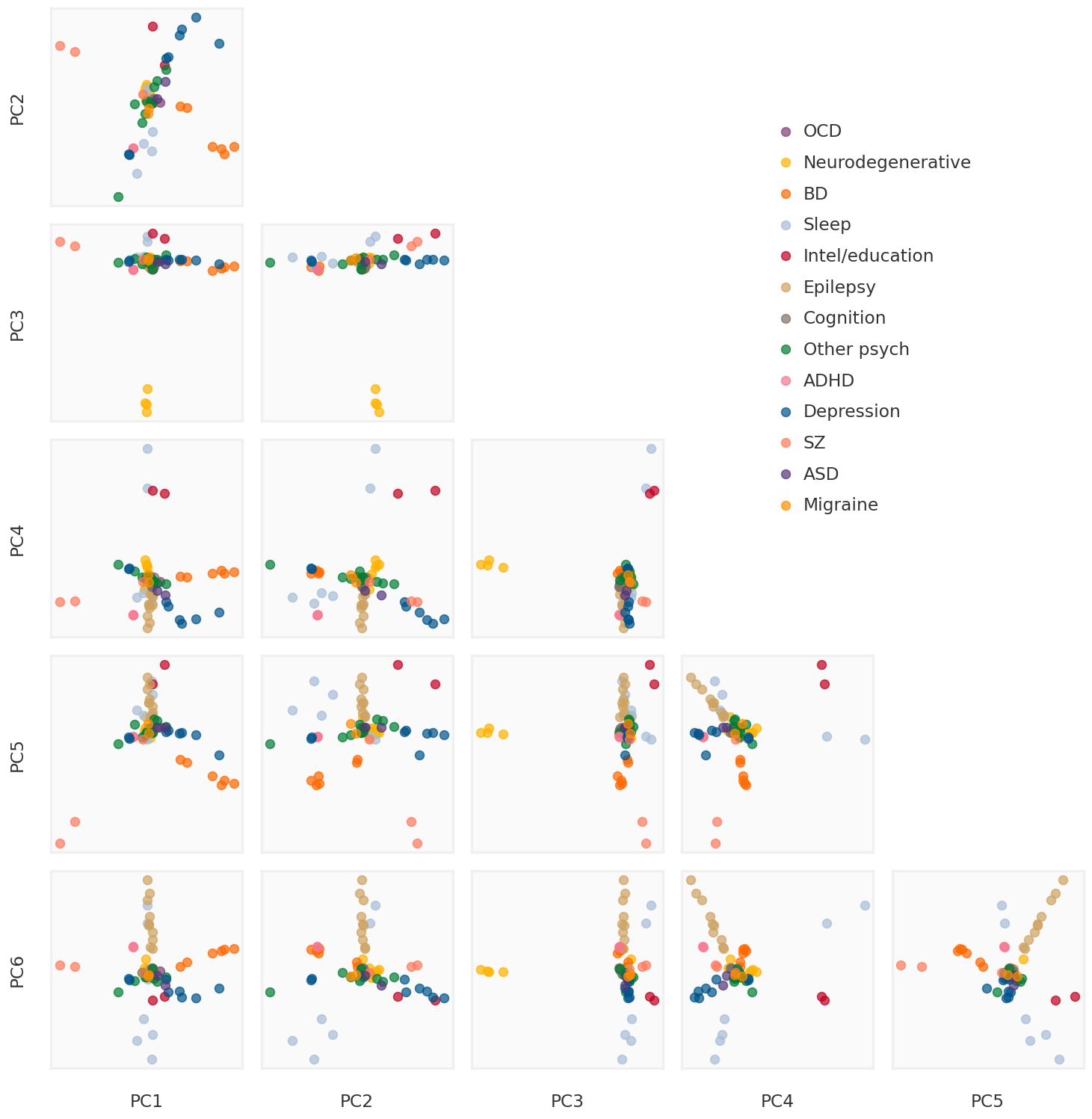
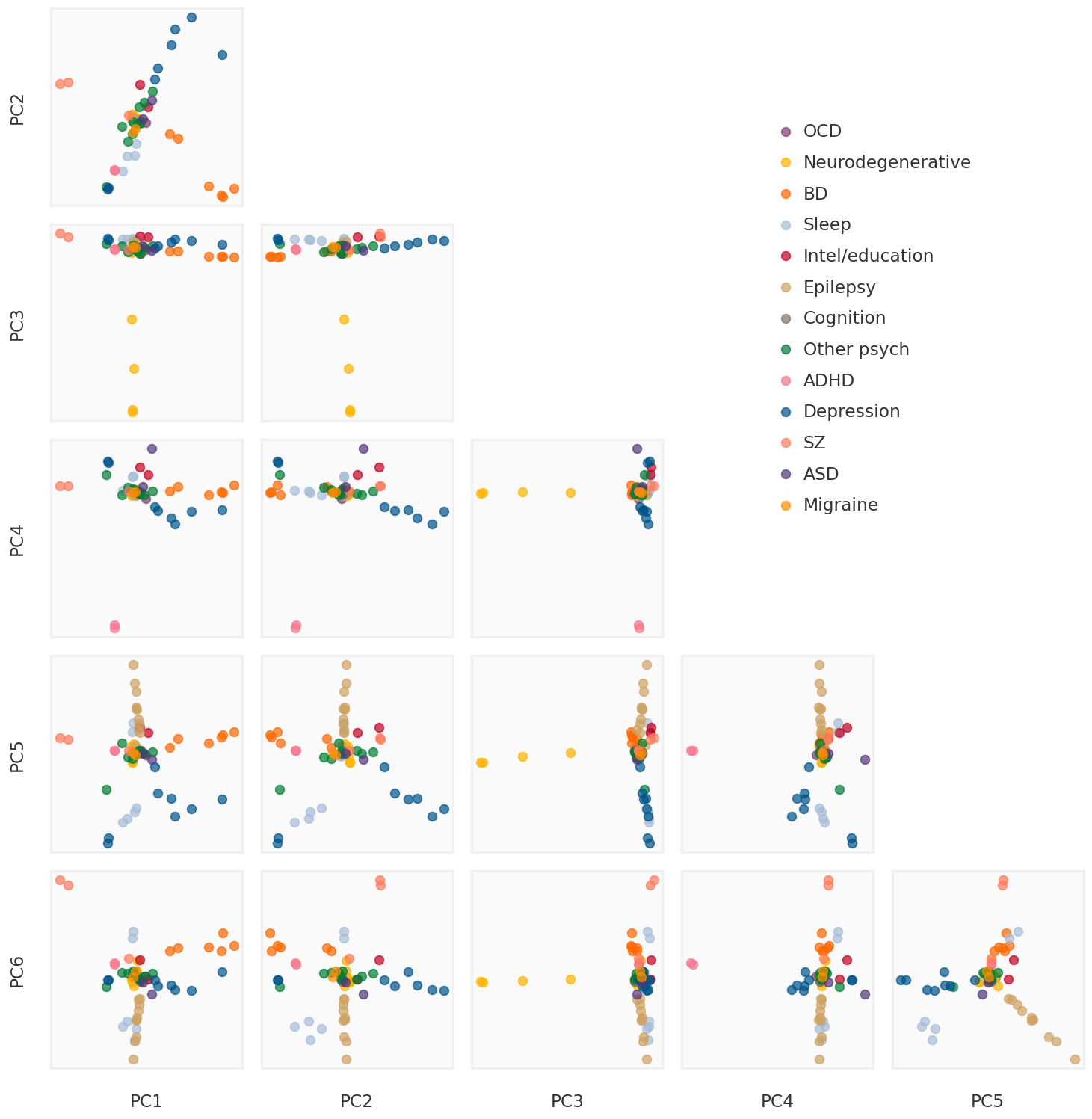
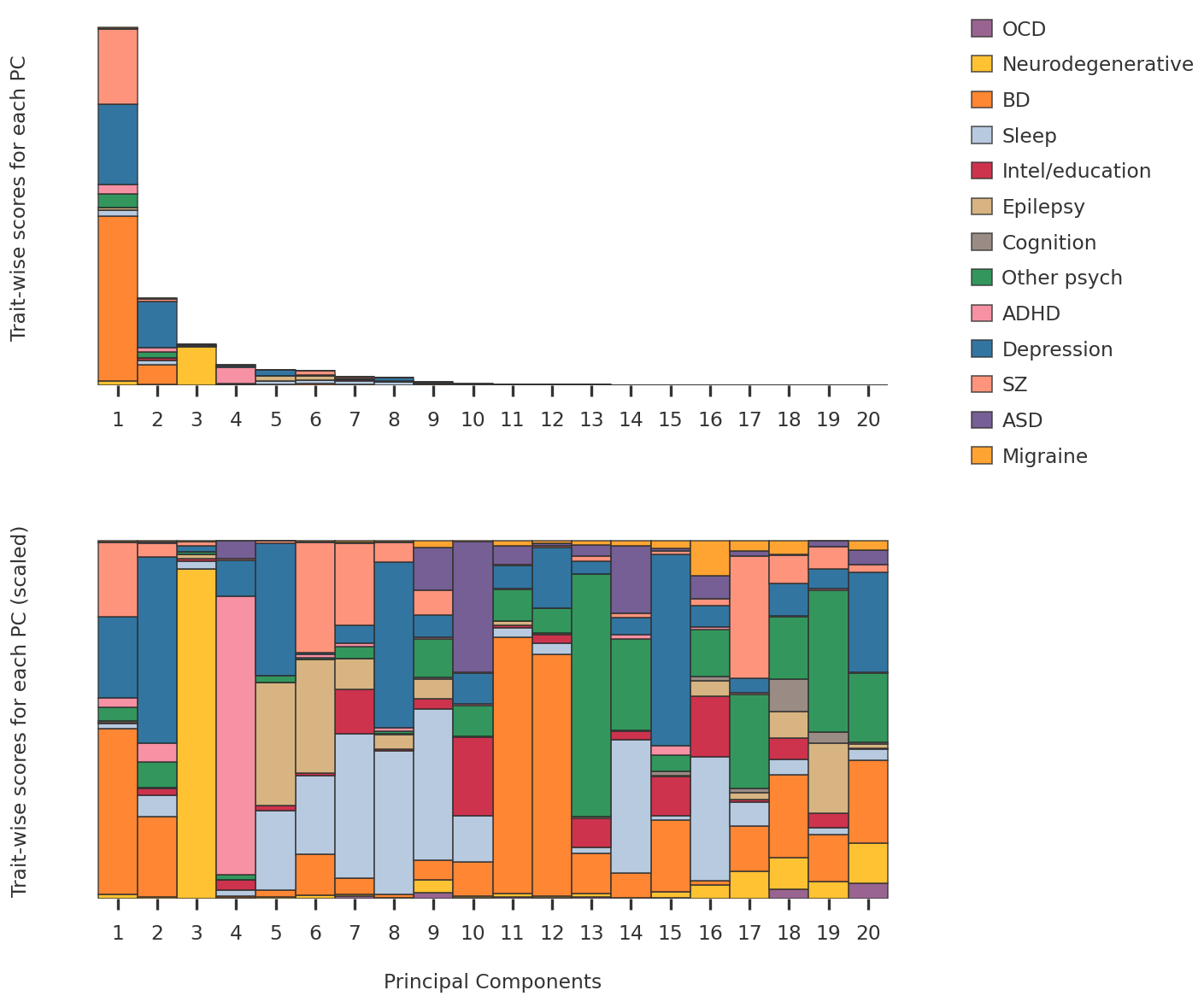
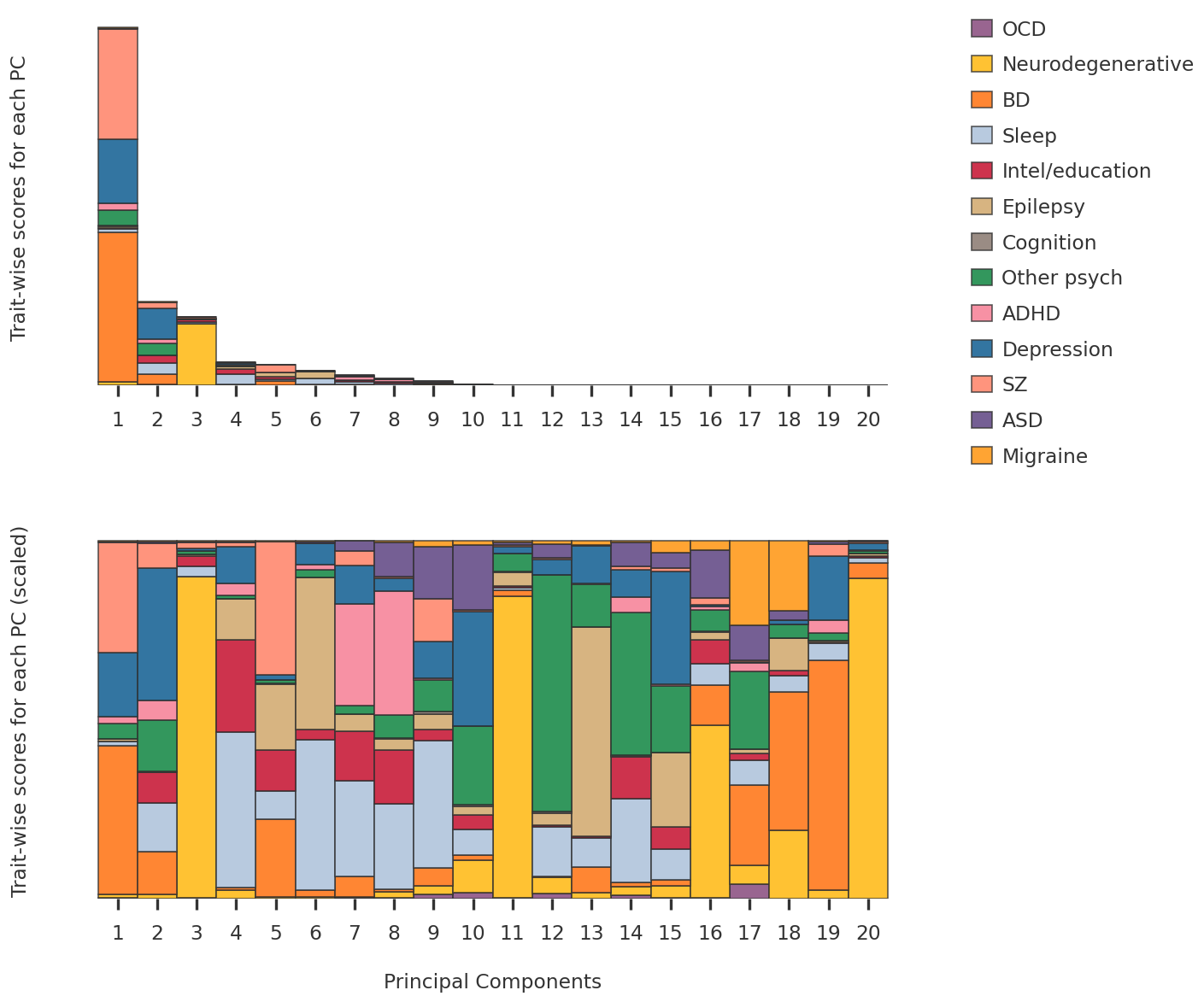
2023-08-08 23:54:07,309 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Cross-validation over 14 ranks.
2023-08-08 23:54:07,338 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Fold 1 ...
2023-08-08 23:54:07,359 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1.0000
2023-08-08 23:54:09,099 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2.0000
2023-08-08 23:54:10,281 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4.0000
2023-08-08 23:54:14,327 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8.0000
2023-08-08 23:54:15,509 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 16.0000
2023-08-08 23:54:17,192 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 32.0000
2023-08-08 23:54:21,295 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 64.0000
2023-08-08 23:54:40,008 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 128.0000
2023-08-08 23:55:00,369 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 256.0000
2023-08-08 23:55:49,015 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 512.0000
2023-08-08 23:56:26,738 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1024.0000
2023-08-08 23:59:33,286 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2048.0000
2023-08-09 00:04:42,654 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4096.0000
2023-08-09 00:11:05,668 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8192.0000
2023-08-09 00:13:31,487 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Fold 2 ...
2023-08-09 00:13:31,526 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1.0000
2023-08-09 00:13:32,692 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2.0000
2023-08-09 00:13:33,858 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4.0000
2023-08-09 00:13:35,041 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8.0000
2023-08-09 00:13:36,189 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 16.0000
2023-08-09 00:13:39,628 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 32.0000
2023-08-09 00:13:44,260 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 64.0000
2023-08-09 00:14:00,394 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 128.0000
2023-08-09 00:14:48,814 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 256.0000
2023-08-09 00:15:04,288 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 512.0000
2023-08-09 00:15:29,648 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1024.0000
2023-08-09 00:17:34,640 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2048.0000
2023-08-09 00:22:51,611 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4096.0000
2023-08-09 00:28:55,921 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8192.0000
2023-08-09 00:31:24,474 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Fold 3 ...
2023-08-09 00:31:24,505 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1.0000
2023-08-09 00:31:25,651 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2.0000
2023-08-09 00:31:26,832 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4.0000
2023-08-09 00:31:28,004 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8.0000
2023-08-09 00:31:32,073 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 16.0000
2023-08-09 00:31:33,801 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 32.0000
2023-08-09 00:31:37,232 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 64.0000
2023-08-09 00:31:46,521 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 128.0000
2023-08-09 00:33:12,132 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 256.0000
2023-08-09 00:33:19,179 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 512.0000
2023-08-09 00:34:26,927 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1024.0000
2023-08-09 00:37:17,619 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2048.0000
2023-08-09 00:42:23,640 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4096.0000
2023-08-09 00:48:33,828 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8192.0000
2023-08-09 00:51:02,371 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Fold 4 ...
2023-08-09 00:51:02,394 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1.0000
2023-08-09 00:51:03,577 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2.0000
2023-08-09 00:51:04,724 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4.0000
2023-08-09 00:51:06,453 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8.0000
2023-08-09 00:51:07,619 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 16.0000
2023-08-09 00:51:09,221 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 32.0000
2023-08-09 00:51:10,957 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 64.0000
2023-08-09 00:51:20,711 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 128.0000
2023-08-09 00:52:36,563 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 256.0000
2023-08-09 00:52:50,815 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 512.0000
2023-08-09 00:54:04,960 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1024.0000
2023-08-09 00:56:22,779 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2048.0000
2023-08-09 01:01:47,072 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4096.0000
2023-08-09 01:08:15,284 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8192.0000
2023-08-09 01:10:46,516 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Fold 5 ...
2023-08-09 01:10:46,547 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1.0000
2023-08-09 01:10:47,748 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2.0000
2023-08-09 01:10:48,947 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4.0000
2023-08-09 01:10:50,135 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8.0000
2023-08-09 01:10:51,338 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 16.0000
2023-08-09 01:10:53,128 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 32.0000
2023-08-09 01:10:56,105 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 64.0000
2023-08-09 01:11:09,642 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 128.0000
2023-08-09 01:12:05,863 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 256.0000
2023-08-09 01:12:17,409 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 512.0000
2023-08-09 01:12:58,131 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 1024.0000
2023-08-09 01:15:24,342 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 2048.0000
2023-08-09 01:21:14,873 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 4096.0000
2023-08-09 01:27:29,020 | nnwmf.optimize.frankwolfe_cv             | DEBUG   | Rank 8192.0000

We do a 5-fold cross-validation. We randomly mask a part of the data and apply our method to recover the masked data. The test error is the RMSE between the receovered data and input masked data. In Figure 4, we plot the RMSE of the test data for each CV fold.

Code 
fig = plt.figure()
ax1 = fig.add_subplot(111)
for k in range(5):
    ax1.plot(np.log10(list(nnmcv.test_error.keys())), [x[k] for x in nnmcv.test_error.values()], 'o-')
ax1.set_xlabel("Rank")
ax1.set_ylabel("RMSE on test data")
mpl_utils.set_xticks(ax1, scale = 'log10', spacing = 'log2')
plt.show()
Figure 4: Error on held out test data for each of the 5-fold cross-validation sets to find the best rank constraint for NNM
Code 
np.linalg.norm(X_cent, 'nuc')
7274.4182279699835
Code 
nnm = FrankWolfe(model = 'nnm', svd_max_iter = 50, show_progress = True, debug = True)
nnm.fit(X_cent, 1024.0)
2023-08-09 10:37:56,367 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 0. Step size 0.459. Duality Gap 481580
2023-08-09 10:38:52,567 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 100. Step size 0.007. Duality Gap 7151
2023-08-09 10:39:49,462 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 200. Step size 0.007. Duality Gap 5557.79
2023-08-09 10:40:46,524 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 300. Step size 0.002. Duality Gap 1879.71

NNMSparse - FW

Code 
nnm_sparse = FrankWolfe(model = 'nnm-sparse', max_iter = 1000, svd_max_iter = 50, 
                        tol = 1e-3, step_tol = 1e-5, simplex_method = 'sort',
                        show_progress = True, debug = True, print_skip = 100)
nnm_sparse.fit(X_cent, (1024.0, 0.5))
2023-08-09 11:18:55,842 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 0. Step size 1.000. Duality Gap 1.13739e+07
2023-08-09 11:20:58,655 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 100. Step size 0.004. Duality Gap 3961.77
2023-08-09 11:23:02,637 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 200. Step size 0.002. Duality Gap 2424.21
2023-08-09 11:25:05,620 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 300. Step size 0.002. Duality Gap 1759.04
2023-08-09 11:27:09,644 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 400. Step size 0.001. Duality Gap 1295.86
2023-08-09 11:29:13,135 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 500. Step size 0.001. Duality Gap 1060.19
2023-08-09 11:31:17,120 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 600. Step size 0.001. Duality Gap 1058.08
2023-08-09 11:33:20,274 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 700. Step size 0.002. Duality Gap 1046.78
2023-08-09 11:35:24,039 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 800. Step size 0.001. Duality Gap 849.241
2023-08-09 11:37:26,504 | nnwmf.optimize.frankwolfe                | INFO    | Iteration 900. Step size 0.001. Duality Gap 944.618
Code 
loadings = Vt.T @ np.diag(S)
loadings[:, 0].shape
(10068,)

Results

Principal Components Biplots

Suppose, we decompose \mathbf{X} = \mathbf{U}\mathbf{S}\mathbf{V}^{\intercal}. Columns of \mathbf{V} are the principal axes (aka principal directions, aka eigenvectors). The principal components are the columns of \mathbf{U}\mathbf{S} – the projections of the data on the the principal axes (note \mathbf{X}\mathbf{V} = \mathbf{U}\mathbf{S}). We plot the principal components as a scatter plot and color each point based on their broad disease category. To show the directions, we plot the loadings, \mathbf{V}\mathbf{S} as arrows. That is, the (x, y) coordinates of an i-th arrow endpoint are given by the i-th value in the first and second column of \mathbf{V}\mathbf{S}.

A comprehensive discussion of biplot on Stackoverflow

Code 
def get_principal_components(X):
    X_cent = mpy_simulate.do_standardize(X, scale = False)
    X_cent /= np.sqrt(np.prod(X_cent.shape))
    U, S, Vt = np.linalg.svd(X_cent, full_matrices = False)
    pcomps = U @ np.diag(S)
    loadings = Vt.T @ np.diag(S)
    return loadings, pcomps

loadings_rpca,       pcomps_rpca = get_principal_components(rpca.L_)
loadings_nnm,        pcomps_nnm = get_principal_components(nnm.X)
loadings_nnm_sparse, pcomps_nnm_sparse = get_principal_components(nnm_sparse.X)
Code 
axmain, axs = mpy_plotfn.plot_principal_components(pcomps_rpca, labels, unique_labels)
plt.show()

Code 
axmain, axs = mpy_plotfn.plot_principal_components(pcomps_nnm, labels, unique_labels)
plt.show()

Code 
axmain, axs = mpy_plotfn.plot_principal_components(pcomps_nnm_sparse, labels, unique_labels)
plt.show()

Code 
quick_plot_trait_pc_scores(nnm_sparse.X, trait_indices, unique_labels, trait_colors)

Code 
quick_plot_trait_pc_scores(nnm.X, trait_indices, unique_labels, trait_colors)

Code 
quick_plot_trait_pc_scores(rpca.L_, trait_indices, unique_labels, trait_colors)

Code 
def quick_scale_plot_trait_pc_scores(ax, X, tindices, ulabels, tcolors, min_idx = 0, max_idx = 20):
    '''
    Quick helper function to plot the same thing many times
    '''
    X_cent = mpy_simulate.do_standardize(X, scale = False)
    U, S, Vt = np.linalg.svd(X_cent, full_matrices = False)
    
    #data = get_trait_pc_scores(U, S, tindices, ulabels, min_idx = min_idx, max_idx = max_idx, use_proportion = False)
    data_scaled = get_trait_pc_scores(U, S, tindices, ulabels, min_idx = min_idx, max_idx = max_idx, use_proportion = True)
    xlabels = [f"{i + 1}" for i in np.arange(min_idx, max_idx)]
    plot_stacked_bars(ax, data_scaled, xlabels, tcolors, alpha = 0.8)

    ax.set_xlabel("Principal Components")
    ax.set_ylabel("Trait-wise scores for each PC (scaled)")
    return

fig = plt.figure(figsize = (12, 14))
ax1 = fig.add_subplot(311)
ax2 = fig.add_subplot(312)
ax3 = fig.add_subplot(313)

quick_scale_plot_trait_pc_scores(ax1, rpca.L_, trait_indices, unique_labels, trait_colors)
quick_scale_plot_trait_pc_scores(ax2, nnm.X, trait_indices, unique_labels, trait_colors)
quick_scale_plot_trait_pc_scores(ax3, nnm_sparse.X, trait_indices, unique_labels, trait_colors)
ax1.legend(bbox_to_anchor=(1.04, 1), loc="upper left")
ax1.set_title("RPCA - IALM")

ax2.set_title("NNM - FW")
ax3.set_title("NNM Sparse - FW")

plt.tight_layout(h_pad = 2.0)
plt.show()