Here I develop the Python class for weighted nuclear norm minimization using Frank-Wolfe algorithm. This is not properly documented, but I keep this notebook for future reference.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pymir import mpl_stylesheet
from pymir import mpl_utils
mpl_stylesheet.banskt_presentation(splinecolor = 'black', dpi = 120, colors = 'kelly')
import sys
sys.path.append("../utils/")
import histogram as mpy_histogram
import simulate as mpy_simulate
import plot_functions as mpy_plotfnntrait = 4 # categories / class
ngwas = 500 # N
nsnp = 1000 # P
nfctr = 40 # KY, Y_true, L, F, mean, noise_var, sample_indices = mpy_simulate.simulate(ngwas, nsnp, ntrait, nfctr, std = 0.5, do_shift_mean = False)
Y_cent = mpy_simulate.do_standardize(Y, scale = False)
Y_std = mpy_simulate.do_standardize(Y)fig = plt.figure(figsize = (8, 8))
ax1 = fig.add_subplot(111)
mpy_plotfn.plot_covariance_heatmap(ax1, L)
plt.tight_layout()
plt.show()
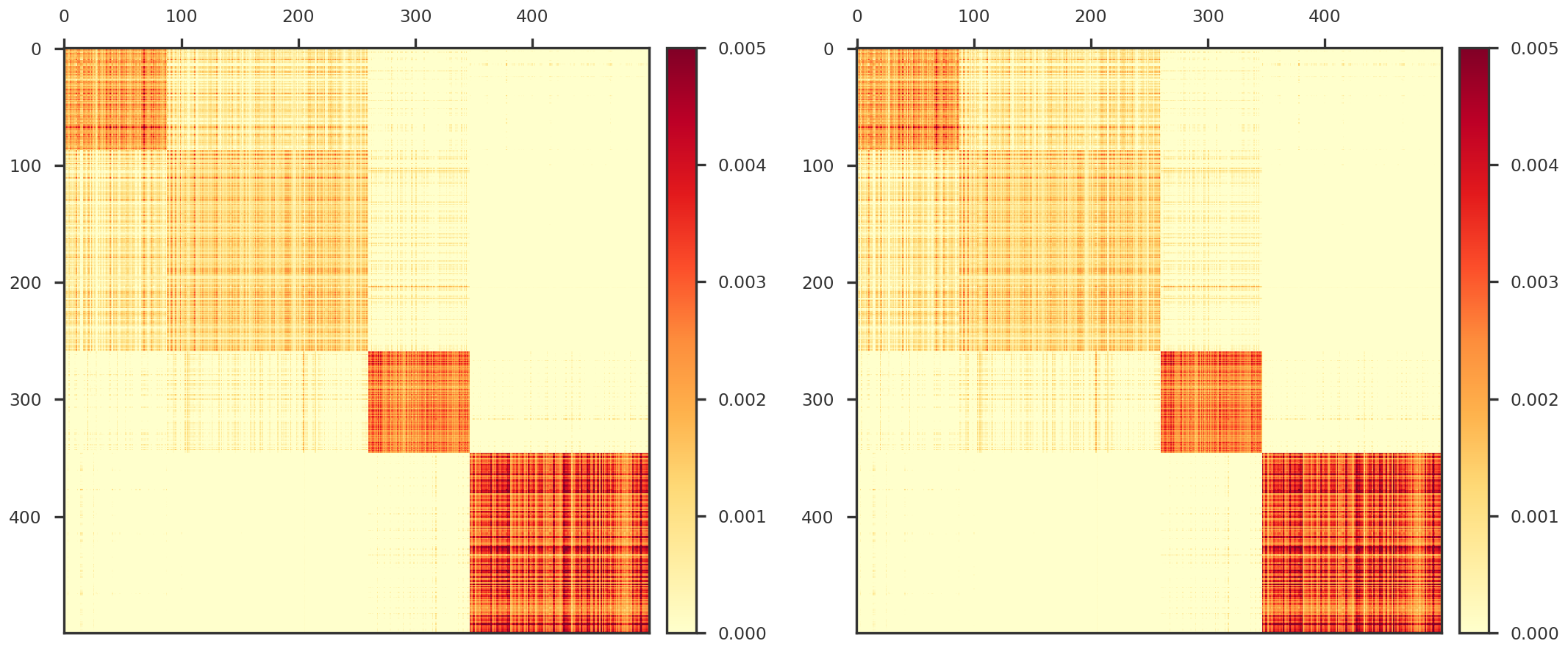
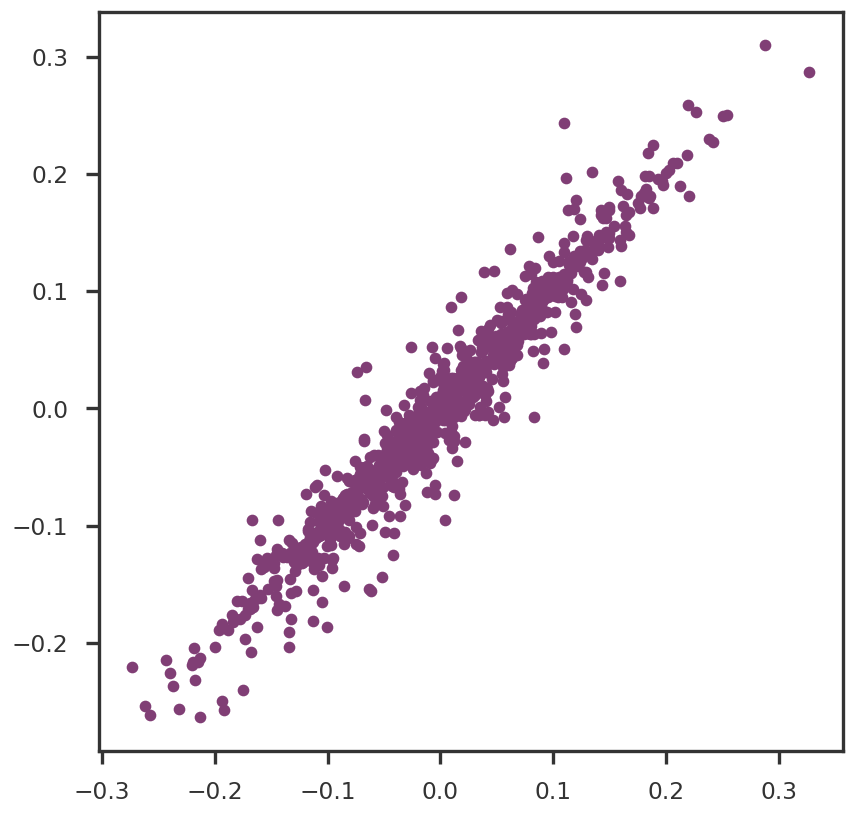
np.linalg.matrix_rank(Y_true)40np.linalg.matrix_rank(Y_cent)499np.linalg.norm(Y_cent, ord = 'nuc')6916.216191017533np.linalg.norm(Y_std, ord = 'nuc')13488.398215158779np.linalg.norm(Y_true, ord = 'nuc')562.4856656633167from sklearn.utils.extmath import randomized_svd
def nuclear_norm(X):
'''
Nuclear norm of input matrix
'''
return np.sum(np.linalg.svd(X)[1])
def f_objective(X, Y, W = None, mask = None):
'''
Objective function
Y is observed, X is estimated
W is the weight of each observation.
'''
Xmask = X if mask is None else X * mask
Wmask = W if mask is None else W * mask
# The * operator can be used as a shorthand for np.multiply on ndarrays.
if Wmask is None:
f_obj = 0.5 * np.linalg.norm(Y - Xmask, 'fro')**2
else:
f_obj = 0.5 * np.linalg.norm(Wmask * (Y - Xmask), 'fro')**2
return f_obj
def f_gradient(X, Y, W = None, mask = None):
'''
Gradient of the objective function.
'''
Xmask = X if mask is None else X * mask
Wmask = W if mask is None else W * mask
if Wmask is None:
f_grad = Xmask - Y
else:
f_grad = np.square(Wmask) * (Xmask - Y)
return f_grad
def linopt_oracle(grad, r = 1.0, max_iter = 10, method = 'power'):
'''
Linear optimization oracle,
where the feasible region is a nuclear norm ball for some r
'''
if method == 'power':
U1, V1_T = singular_vectors_power_method(grad, max_iter = max_iter)
elif method == 'randomized':
U1, V1_T = singular_vectors_randomized_method(grad, max_iter = max_iter)
S = - r * U1 @ V1_T
return S
def singular_vectors_randomized_method(X, max_iter = 10):
u, s, vh = randomized_svd(X, n_components = 1, n_iter = max_iter,
power_iteration_normalizer = 'none',
random_state = 0)
return u, vh
def singular_vectors_power_method(X, max_iter = 10):
'''
Power method.
Computes approximate top left and right singular vector.
Parameters:
-----------
X : array {m, n},
input matrix
max_iter : integer, optional
number of steps
Returns:
--------
u, v : (n, 1), (p, 1)
two arrays representing approximate top left and right
singular vectors.
'''
n, p = X.shape
u = np.random.normal(0, 1, n)
u /= np.linalg.norm(u)
v = X.T.dot(u)
v /= np.linalg.norm(v)
for _ in range(max_iter):
u = X.dot(v)
u /= np.linalg.norm(u)
v = X.T.dot(u)
v /= np.linalg.norm(v)
return u.reshape(-1, 1), v.reshape(1, -1)
def do_step_size(dg, D, W = None, old_step = None):
if W is None:
denom = np.linalg.norm(D, 'fro')**2
else:
denom = np.linalg.norm(W * D, 'fro')**2
step_size = dg / denom
step_size = min(step_size, 1.0)
if step_size < 0:
print ("Warning: Step Size is less than 0")
if old_step is not None and old_step > 0:
print ("Using previous step size")
step_size = old_step
else:
step_size = 1.0
return step_size
def frank_wolfe_minimize_step(X, Y, r, istep, W = None, mask = None, old_step = None, svd_iter = None, svd_method = 'power'):
# 1. Gradient for X_(t-1)
G = f_gradient(X, Y, W = W, mask = mask)
# 2. Linear optimization subproblem
if svd_iter is None:
svd_iter = 10 + int(istep / 20)
svd_iter = min(svd_iter, 25)
S = linopt_oracle(G, r, max_iter = svd_iter, method = svd_method)
# 3. Define D
D = X - S
# 4. Duality gap
dg = np.trace(D.T @ G)
# 5. Step size
step = do_step_size(dg, D, W = W, old_step = old_step)
# 6. Update
Xnew = X - step * D
return Xnew, G, dg, step
def frank_wolfe_minimize(Y, r, X0 = None,
weight = None,
mask = None,
max_iter = 1000,
svd_iter = None,
svd_method = 'power',
tol = 1e-4, step_tol = 1e-3, rel_tol = 1e-8,
return_all = True,
debug = False, debug_step = 10):
# Step 0
old_X = np.zeros_like(Y) if X0 is None else X0.copy()
dg = np.inf
step = 1.0
if return_all:
dg_list = [dg]
fx_list = [f_objective(old_X, Y, W = weight, mask = mask)]
st_list = [1]
# Steps 1, ..., max_iter
for istep in range(max_iter):
X, G, dg, step = \
frank_wolfe_minimize_step(old_X, Y, r, istep, W = weight, mask = mask, old_step = step, svd_iter = svd_iter, svd_method = svd_method)
f_obj = f_objective(X, Y, W = weight, mask = mask)
fx_list.append(f_obj)
if return_all:
dg_list.append(dg)
st_list.append(step)
if debug:
if (istep % debug_step == 0):
print (f"Iteration {istep}. Step size {step:.3f}. Duality Gap {dg:g}")
# Stopping criteria
# duality gap
if np.abs(dg) <= tol:
break
# step size
if step > 0 and step <= step_tol:
break
# relative tolerance of objective function
f_rel = np.abs((f_obj - fx_list[-2]) / f_obj)
if f_rel <= rel_tol:
break
old_X = X.copy()
if return_all:
return X, dg_list, fx_list, st_list
else:
return Xfrom sklearn.utils.extmath import randomized_svd
class TopCompSVD():
def __init__(self, method = 'power', max_iter = 10):
self._method = method
self._max_iter = max_iter
return
def fit(self, X):
if self._method == 'power':
self._u1, self._v1h = self.fit_power(X)
elif self._method == 'randomized':
self._u1, self._v1h = self.fit_randomized(X)
return
def fit_power(self, X):
n, p = X.shape
u = np.random.normal(0, 1, n)
u /= np.linalg.norm(u)
v = X.T.dot(u)
v /= np.linalg.norm(v)
for _ in range(self._max_iter):
u = X.dot(v)
u /= np.linalg.norm(u)
v = X.T.dot(u)
v /= np.linalg.norm(v)
return u.reshape(-1, 1), v.reshape(1, -1)
def fit_randomized(self, X):
u, s, vh = sp.randomized_svd(X,
n_components = 1, n_iter = self._max_iter,
power_iteration_normalizer = 'none',
random_state = 0)
return u, vh
@property
def u1(self):
return self._u1
@property
def v1_t(self):
return self._v1h
class NNMFW():
def __init__(self, max_iter = 1000,
svd_method = 'power', svd_max_iter = None,
stop_criteria = ['duality_gap', 'step_size', 'relative_objective'],
tol = 1e-3, step_tol = 1e-3, rel_tol = 1e-8,
show_progress = False, print_skip = None,
debug = True):
self._max_iter = max_iter
self._svd_method = svd_method
self._svd_max_iter = svd_max_iter
self._stop_criteria = stop_criteria
self._tol = tol
self._step_size_tol = step_tol
self._fxrel_tol = rel_tol
self._show_progress = show_progress
self._prog_step_skip = print_skip
if self._show_progress and self._prog_step_skip is None:
self._prog_step_skip = max(1, int(self._max_iter / 100)) * 10
self._debug = debug
return
def f_objective(self, X):
'''
Objective function
Y is observed, X is estimated
W is the weight of each observation.
'''
Xmask = self.get_masked(X)
# The * operator can be used as a shorthand for np.multiply on ndarrays.
if self._weight_mask is None:
fx = 0.5 * np.linalg.norm(self._Y - Xmask, 'fro')**2
else:
fx = 0.5 * np.linalg.norm(self._weight_mask * (self._Y - Xmask), 'fro')**2
return fx
def f_gradient(self, X):
'''
Gradient of the objective function.
'''
Xmask = self.get_masked(X)
if self._weight_mask is None:
gx = Xmask - self._Y
else:
gx = np.square(self._weight_mask) * (Xmask - self._Y)
return gx
def fw_step_size(self, dg, D):
if self._weight_mask is None:
denom = np.linalg.norm(D, 'fro')**2
else:
denom = np.linalg.norm(self._weight_mask * D, 'fro')**2
ss = dg / denom
ss = min(ss, 1.0)
if ss < 0:
print("Step Size is less than 0. Using last valid step size.")
ss = self._st_list[-1]
return ss
def get_masked(self, X):
if self._mask is None or X is None:
return X
else:
return X * self._mask
def linopt_oracle(self, X):
'''
Linear optimization oracle,
where the feasible region is a nuclear norm ball for some r
'''
U1, V1_T = self.get_singular_vectors(X)
S = - self._rank * U1 @ V1_T
return S
def get_singular_vectors(self, X):
max_iter = self._svd_max_iter
if max_iter is None:
nstep = len(self._st_list) + 1
max_iter = 10 + int(nstep / 20)
max_iter = min(max_iter, 25)
svd = TopCompSVD(method = self._svd_method, max_iter = max_iter)
svd.fit(X)
return svd.u1, svd.v1_t
def fit(self, Y, r, weight = None, mask = None, X0 = None):
'''
Wrapper function for the minimization
'''
n, p = Y.shape
# Make some variables available for the class
self._weight = weight
self._mask = mask
self._weight_mask = self.get_masked(self._weight)
self._Y = Y
self._rank = r
# Step 0
X = np.zeros_like(Y) if X0 is None else X0.copy()
dg = np.inf
step = 1.0
fx = self.f_objective(X)
# Save relevant variables in list
self._dg_list = [dg]
self._fx_list = [fx]
self._st_list = [step]
# Steps 1, ..., max_iter
for i in range(self._max_iter):
X, G, dg, step = self.fw_one_step(X)
fx = self.f_objective(X)
self._fx_list.append(fx)
self._dg_list.append(dg)
self._st_list.append(step)
if self._show_progress:
if (i % self._prog_step_skip == 0):
print (f"Iteration {i}. Step size {step:.3f}. Duality Gap {dg:g}")
if self.do_stop():
break
self._X = X
return
def fw_one_step(self, X):
# 1. Gradient for X_(t-1)
G = self.f_gradient(X)
# 2. Linear optimization subproblem
S = self.linopt_oracle(G)
# 3. Define D
D = X - S
# 4. Duality gap
dg = np.trace(D.T @ G)
# 5. Step size
step = self.fw_step_size(dg, D)
# 6. Update
Xnew = X - step * D
return Xnew, G, dg, step
def do_stop(self):
# self._stop_criteria = ['duality_gap', 'step_size', 'relative_objective']
#
if 'duality_gap' in self._stop_criteria:
dg = self._dg_list[-1]
if np.abs(dg) <= self._tol:
return True
#
if 'step_size' in self._stop_criteria:
ss = self._st_list[-1]
if ss <= self._step_size_tol:
return True
#
if 'relative_objective' in self._stop_criteria:
fx = self._fx_list[-1]
fx0 = self._fx_list[-2]
fx_rel = np.abs((fx - fx0) / fx0)
if fx_rel <= self._fxrel_tol:
return True
#
return FalseX_opt, dg_list, fx_list, step_list = frank_wolfe_minimize(Y_cent, 40.0, max_iter = 1000, debug = True, debug_step = 100, step_tol = 1e-4, svd_iter=100)Iteration 0. Step size 1.000. Duality Gap 2528.37
Warning: Step Size is less than 0
Using previous step size
Warning: Step Size is less than 0
Using previous step sizefig = plt.figure(figsize = (14, 6))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
kp = len(step_list)
fx_arr = np.array(fx_list)
fx_rel_diff_log10 = np.log10(np.abs(np.diff(fx_arr) / fx_arr[1:]))
ax1.plot(np.arange(kp - 2), dg_list[2:kp])
# ax2.plot(np.arange(kp - 1), np.log10(fx_list[1:kp]))
ax2.plot(np.arange(kp - 1), fx_rel_diff_log10)
ax1.set_xlabel("Number of iterations")
ax2.set_xlabel("Number of iterations")
ax1.set_ylabel(r"Duality gap, $g_t$")
ax2.set_ylabel(r"Objective function, $f(\mathbf{X})$")
fig.tight_layout(w_pad = 2.0)
plt.show()
nnm = NNMFW(show_progress = True, svd_max_iter = 50)
nnm.fit(Y_cent, 40.0)Iteration 0. Step size 1.000. Duality Gap 2528.37
Step Size is less than 0. Using last valid step size.nnm._st_list[1.0,
1.0,
0.4059508526803153,
0.19713776422660786,
0.031601077477726426,
0.011408112527596072,
0.011435454280280217,
0.011435454280280217,
0.0003653454546090821]nnm._fx_list[68953.79597625589,
67225.42267046764,
66961.74891880063,
66914.56295271001,
66914.19909538413,
66914.12717521715,
66914.04739067073,
66914.16163671855,
66914.16150434242]fx_list[68953.79597625589,
67225.42267046703,
66961.74891743576,
66914.56295259335,
66914.22530475237,
66914.11898081755,
66914.28171754857,
66914.21086735667,
66914.20897738854,
66914.1850500866,
66914.17070820235,
66914.16008819439,
66914.13124317658,
66914.18277041374,
66914.15440484512,
66914.13133305841,
66914.12544153685,
66914.12542199122]U, S, Vt = np.linalg.svd(mpy_simulate.do_standardize(X_opt, scale = False), full_matrices=False)
U1, S1, Vt1 = np.linalg.svd(mpy_simulate.do_standardize(nnm._X, scale = False), full_matrices=False)
fig = plt.figure(figsize = (18, 8))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
mpy_plotfn.plot_covariance_heatmap(ax1, U @ np.diag(S), vmax = 0.005)
mpy_plotfn.plot_covariance_heatmap(ax2, U1 @ np.diag(S1), vmax = 0.005)
plt.tight_layout(w_pad=2.0)
plt.show()
Y_true_cent = mpy_simulate.do_standardize(Y_true, scale = False)def psnr(original, recovered):
n, p = original.shape
maxsig2 = np.square(np.max(original) - np.min(original))
mse = np.sum(np.square(recovered - original)) / (n * p)
res = 10 * np.log10(maxsig2 / mse)
return respsnr(Y_true_cent, X_opt)21.65905757205794psnr(Y_true_cent, nnm._X)21.664554727300995psnr(Y_true_cent, Y_cent)9.943220233648011Y_true_mean = np.mean(Y_true, axis = 0)
Y_obs_mean = np.mean(Y, axis = 0)
fig = plt.figure(figsize = (8, 8))
ax1 = fig.add_subplot(111)
ax1.scatter(Y_true_mean, Y_obs_mean)
plt.show()